|
|
Review Article
| ||||||
| Dental occlusion: A newly proposed tetrahedral theory of occlusion | ||||||
| Adolphus Odogun Loto | ||||||
|
1Senior Lecturer, Department of Restorative Dentistry, Faculty of Dentistry, Lagos State University College of Medicine, Ikeja, Lagos, Nigeria
| ||||||
| ||||||
|
[HTML Abstract]
[PDF Full Text]
[Print This Article]
[Similar article in Pumed] [Similar article in Google Scholar] |
| How to cite this article |
| Loto AO. Dental occlusion: A newly proposed tetrahedral theory of occlusion. Edorium J Dent 2017;4:26–35. |
|
ABSTRACT
|
|
Dental occlusion constitutes an important subject that cuts across many disciplines in the field of dentistry. There have been raging debates on occlusion and articulation with different opinions on theories and concepts. The raging debates have resulted into two schools of thoughts namely: the gnathological school of thought and the neuromuscular school of thought. The objective of this article was to show the interdependence and inter-relationship of the two schools of thought by proposing a new mechanical theory upon which the neuromuscular school of thought can be super-imposed. To this end, a tetrahedron is considered as the unifying geometrical figure upon which the new theory of occlusion is based. Thus, the various established theories and concepts of occlusion can adequately be explained using the tetrahedron’s characteristics. Consequently, a new theory of occlusion to be called the tetrahedral theory of occlusion is hereby presented to the dental professionals for further objective critique. | |
|
Keywords:
Occlusion theories, Neuromuscular, Tetrahedron
| |
|
INTRODUCTION
| ||||||
|
Dental occlusion is a subject that cuts across many disciplines in the field of dentistry owing to its wide rage of applications in diagnostic, preventive and therapeutic procedures. The complex biodynamics of the bite can be analyzed using two main processes – occlusion and articulation. The word occlusion is derived from the Latin word occludere which means, to shut up or close up. Dental occlusion refers to the closure of teeth. Today, however, many definitions have been given by different authors and different interpretations have caused a lot of confusion in understanding the subject. Taber’s Cyclopedic Medical Dictionary defines dental occlusion as the relation of the teeth when the jaws are closed [1]. Jablonski’s illustrated dictionary defines occlusion as the relationship between all the components of the masticatory system in normal function, dysfunction and parafunction, including the morphology and functional features of contacting surfaces of opposing teeth and restorations, occlusal trauma and dysfunction, neuromuscular physiology, the temporomandibular joint and muscle function, swallowing and mastication, psycho-physiological status and the diagnosis, prevention and treatment of functional disorders of the masticatory system [2]. The term articulation includes all types of position of the lower jaw in relation to upper jaw singling out the various phases in the contact relationship of the dental rows. The differentiation of occlusal conditions in the biodynamics of the maxillo-mandibular-dental system is of great theoretical and practical importance. For over a century, dentists and researchers have engaged in many discussions on identification and definition of concepts of dental occlusion that can be applied in diagnostic and therapeutic situations. These discussions have generated many controversies and unanswered questions as to which concept or theory is superior to the other. The controversies still range without ceasing. All occlusal concepts are derivatives of occlusal theories; and all theories might have evolved from the past creative thinking of some researchers. Consequently, the dental profession has been divided into two camps with respect to occlusal philosophy. The first camp is the mechanical school of thought which considers maxillo-mandibular-dental system as an efficient mechanical system; and the design and construction of its hard structural framework is based on its varied functional activities. This school of thought was pioneered by Bonwill using his equilateral triangle theory [3] [4]. Other occlusal theories in gnathological school of thought include Von Spee’s sagittal occlusal curves, [5] Monson’s spherical theory [6][7] and Hall’s conical theory [8][9][10]. Each of these theories has its followership; and the construction of many articulators is based on these theories for diagnostic and therapeutic purposes [11][12][13][14]. The second camp is the neuromuscular school of thought which is concerned with the importance and role of orofacial muscles in shaping occlusal behaviors as well as the functional considerations of orofacial muscles in diagnostic and the therapeutic procedures. The neuromuscular theory was pioneered by Dr. Bernard Jankelson [15][16]. In order to bring the two camps together there is need to have new information and insights. However, this would require continued analysis of our currently recognized concepts, theories and therapeutic approaches to occlusal problems. Consequently, the purpose of this article is to produce a theory that will unify all the well-known theories of occlusion and articulation into single theory that encompasses gnathological and neuromuscular schools of thought through exploration of relevant scientifically based literature on occlusion and articulation. | ||||||
| Hypothesis | ||||||
|
The ‘tetrahedral hypothesis’ of occlusion states that a regular tetrahedron, derived from Bonwill’s equilateral triangle, constitutes the unifying 3D geometrical figure of all well-known theories of occlusion (Bonwill’s equilateral theory of occlusion, Spee’s sagittal curves of occlusion, Monson’s spherical theory of occlusion and Hall’s conical theory of occlusion); and the height of the regular tetrahedron represents the rest vertical dimension. This hypothesis is based on the following assumptions:
| ||||||
| Methodology | ||||||
|
Literature search was carried out using data bases and search engines such as google scholar, Medline plus, PubMed, Cochrane library, free full PDF, Index Copernicus, and worldwide science. During the search, phrases such as Bonwill theory of occlusion, Monson’s spherical theory of occlusion, conical theory of occlusion, equilateral theory of occlusion, occlusal concepts and bio-mechanics of the maxillo-mandibular-dental system, characteristics of equilateral triangle, circle, cone, sphere and tetrahedron were used. Scholarly published articles on occlusion theories from 1864 to 2010 were selected based on the following inclusion criteria:
The exclusion criteria include:
Twenty-five articles, including articles on geometric figures, were selected out of two hundred and fifteen articles based on the aforementioned inclusion and exclusion criteria. The findings from these studies were subjected to critical analysis, synthesis and integration for the purpose of establishing a unifying geometrical figure for all the well-known occlusion theories. | ||||||
| The thinking behind the theory | ||||||
|
This theory is different from the current thinking of theories of occlusion because it is an attempt to unify all well-known theories and concepts of occlusion into single theory. It is also different because a tetrahedron, which is being used as the unifying geometric figure, is a 3D-object that is also intimately associated with circle, sphere, cone and equilateral triangle. The idea of the tetrahedral theory of occlusion evolves from a critical qualitative and quantitative analysis, synthesis and integration of Bonwill’s equilateral triangle, [3][4] Spee’s sagittal occlusal curves, [5] Monson’s spherical theory [6][7], Hall’s conical theory [8][9][10] and Jankelson’s neuromuscular theory [15][16] for the purpose of laying a foundation for the unification of the aforementioned theories of occlusion into single theory that can adequately explain the existing theories. In order to have a good understanding of the interconnectedness of the aforementioned theories, it is important to explain the following terms: Spee’s Curve: This is the curvature of teeth arrangement on the mandible starting from the tip of the canine and running through buccal cusps of the molars and up to the most anterior aspect of the condylar process [4]. Curve: This is an arc which in turn is a part of a circle. Arc: this is a part of the circumference of a circle cut-off by a chord or two radii. Arc: this is a part of the circumference of a circle cut-off by a chord or two radii. Circle: This is the locus of all points in a space say P, equidistant from a fixed point, say O, the fixed point is called the center of the circle while the distance OP is called the radius of the circle. The path traced by the point P around point O is called the perimeter or circumference of the circle. Diameter: This is a chord of a circle which divides the circle into two equal parts. The division is through the centre of the circle. Each part is called a semi-circle. Chord: A chord of a circle is a straight line through a circle and which divides the circle into two parts (whether equal or unequal). When the straight lime divides the circle into two equal parts, then, each part is called a semi-circle. But when the line is not through the centre of the circle, then, the two parts that are formed are not equal. The parts are called segments. The bigger part is called the major segment, while the smaller part is called minor segment. Circumference: This is the perimeter of a circle (distance round a circle). Sphere: This is a set of points in space at a fixed distance from a given fixed point (its centre). The cross section of a sphere is a circle with different radii at different parts on the sphere’s surface. Having explained the aforementioned terms, a logical and scientific interconnectedness amongst the various theories of occlusion are hereby stated as follows: | ||||||
| Formation of Bonwill’s equilateral triangle | ||||||
|
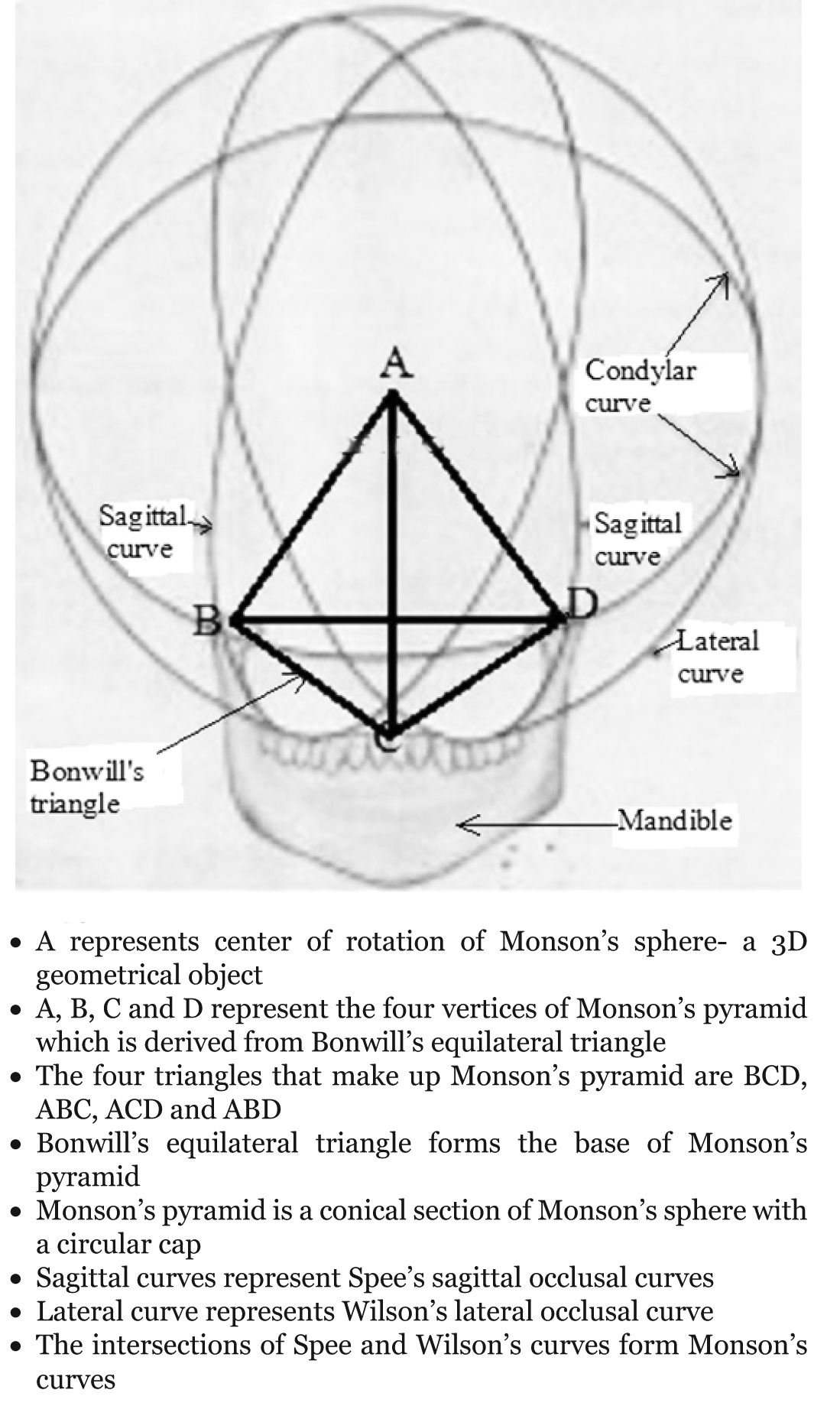
Bonwill [3][4] proposed that mandibular movements are guided by the condylar and incisal guidances; and the teeth move in relation to each other as guided by these guidances. He advanced that the joining of the two condylar processes of the mandible and the incisal point (at the midpoint of the lower central incisors) with straight lines, an equilateral triangle is formed and each side of the triangle is approximately 10 cm. This is known as Bonwill’s equilateral triangle; and it forms the basis of construction of some articulators (Figure 1). | ||||||
| Formation of Spee’s sagittal occlusal curves | ||||||
|
Spee [5] proposed that during protrusive movement of the mandible, the condyles and the teeth describe a common curve which is a part of a circle whose centre is the glabella; and the radius of the circle is about 10 cm. This curve is referred to as sagittal occlusal curve and lies at the lower segment of the circle (Figure 1). A straight line that connects the two-ends of Spee’s curve on one side of the mandible is a chord of a circle whose centre is at the glabella. | ||||||
| Formation of monson sphere and lateral curves | ||||||
|
Monson [6] linked up Spee’s curves with perpendicular bisectors of their whole chords and demonstrated that the bisecting lines intersected at the glabella. He also demonstrated that the co-ordinated forces (resultant force) from the lower teeth also intersected at the glabella. This point of intersection is the centre of a sphere having a radius of about 10 cm; and its lower segment represents the occlusal surface. He further demonstrated the presence of lateral occlusal curves owing to the different levels of the lingual and buccal cusps of posterior teeth (Figure 1). | ||||||
| Formation of Hall’s cone | ||||||
|
Hall [8][9] [10] proposed that the lower teeth move over the surfaces of the upper teeth as over the surfaces of a cone, generating an angle of 45° with the central axis of the cone tipped at 45° to the occlusal plane. The base of the cone lies posterior while its apex is the midpoint of the contact area of the lower central incisors (Figure 1). | ||||||
| Formation of spherical, circular, triangular, and conical geometric topographies by msucles of the oro-facial region | ||||||
|
The orofacial muscles are the working organs of the central nervous system (CNS). They determine the resting state of the mandible, the temporomandibular joints and the teeth by virtue of their tone which is controlled by the central nervous system under the influence of internally and externally generated impulses. The orofacial muscles are all formed of independent groups and are joined into single whole from anatomical point of view and with respect to their final combined complex function. These muscles are arranged in circular, triangular and conical anatomic configurations for the purpose of fulfilling their group and individual functions. The neuromuscular system is organized, in terms of arrangement and orientation, so that the hard framework of the maxillo-mandibular-dental system can effectively and efficiently perform its complex biomechanical functions of swallowing, mastication, speech and other oro-facial expressions. However, the hard framework of the oro-facial region is meaningless without the input of the neuromuscular system; and this was the conclusion of Bernard Jankelson – the father of Neuromuscular theory [15][16]. | ||||||
| Establishing the interconnectedness of Spee’s curves, monson’s sphere and curves, Hall’s cone, Bonwill’s triangle and Jankelson’s neuromuscular theory | ||||||
|
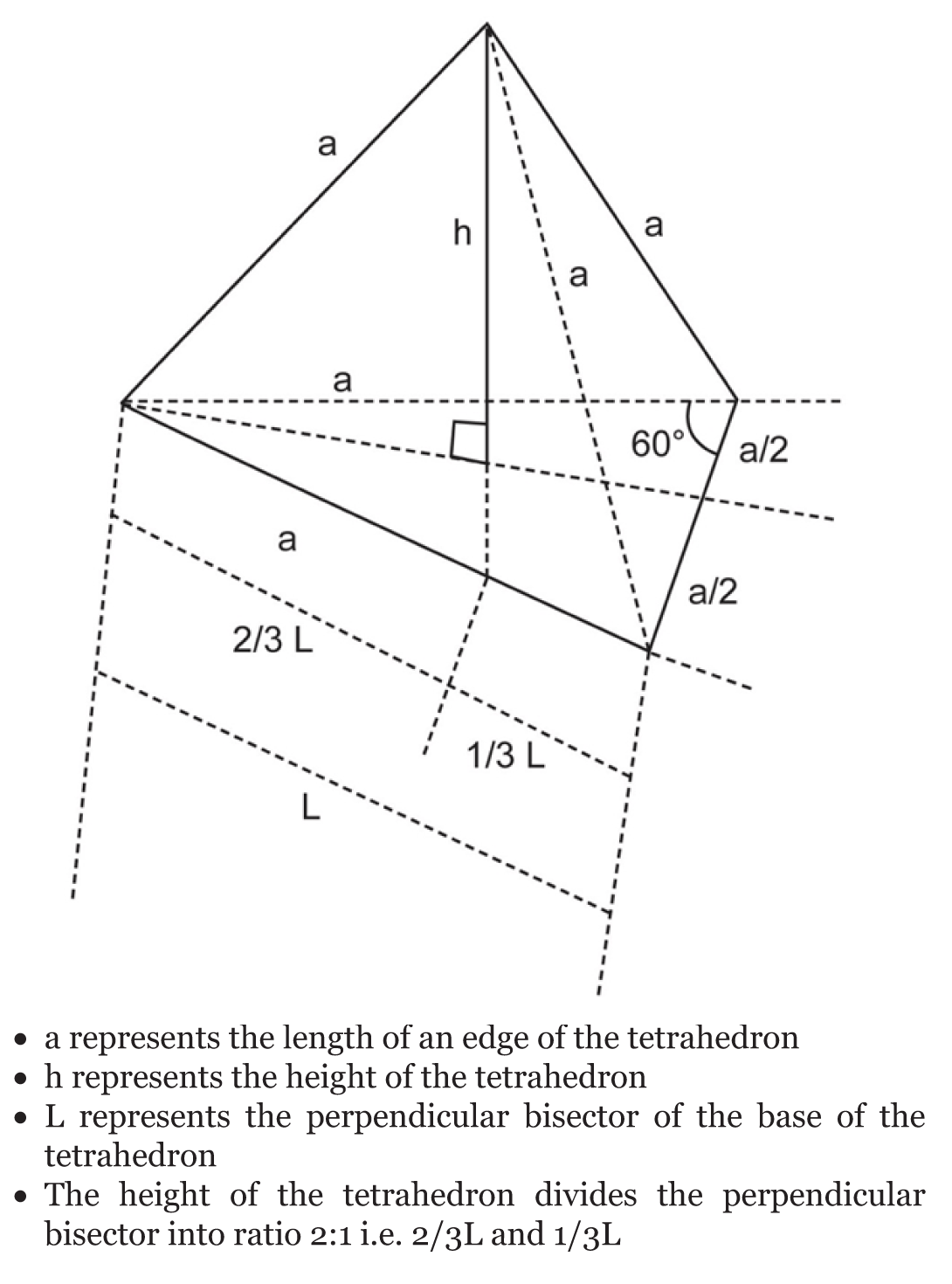
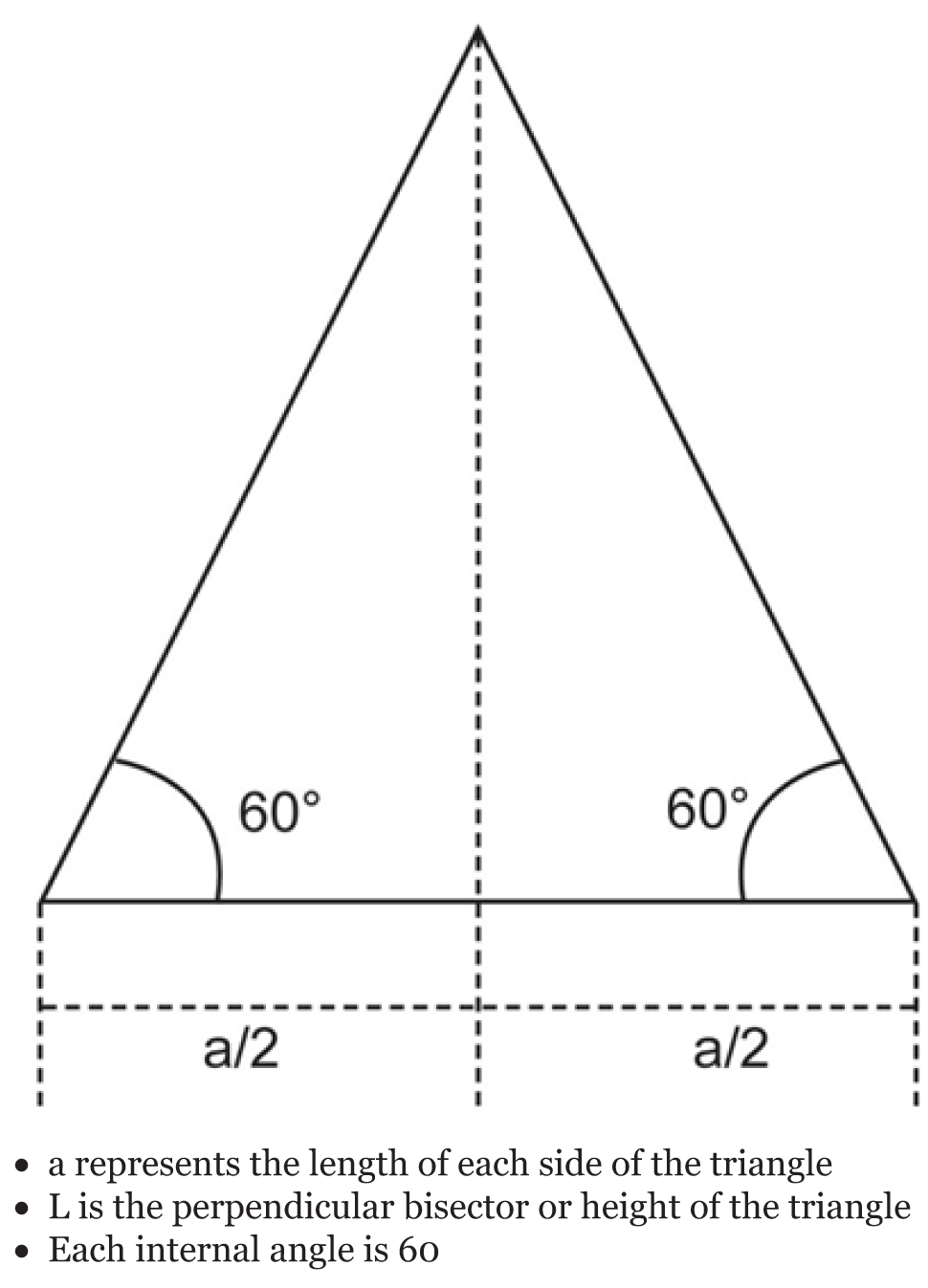
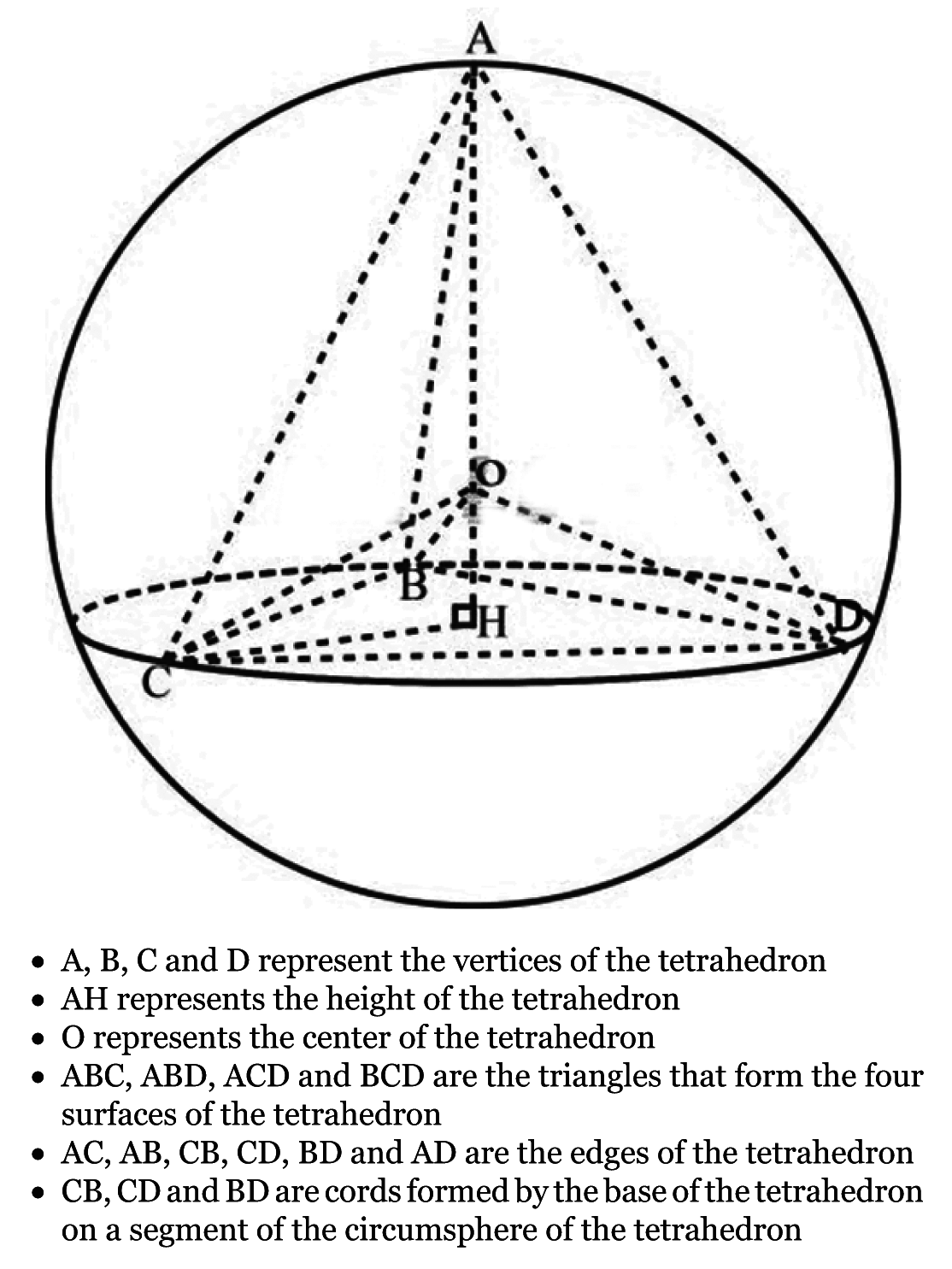
Concerning Bonwill’s triangle, [3][4] that is formed by joining the two condylar processes of the mandible and the incisal point (at the midpoint of the lower central incisors) with straight lines, the right and left sides of the triangle can be regarded as the right and left chords of Spee’s curves [5]. The perpendicular bisectors from the sides of Bonwill’s equilateral triangle also intersect at the point similar to the common centre of rotation of Spee’s circle and Monson’s sphere (Figure 1) [5][6][7]. Therefore, perpendicular lines, drawn upward, from the tree vertices of the Bonwill’s triangle will result in the formation of a regular tetrahedron since all the three sides are of the same length (Figure 1). The tetrahedron can also be regarded as a cone or a pyramid with a triangular base in line with Hall’s cone [8][9][10]. Concerning Spee’s curves, [5] the right and left sides of Bonwill’s triangle [3][4] can be regarded as the extended right and left chords of Spee’s curves. The perpendicular bisectors from these whole chords of Spee’s curves on both sides of the mandible intersect at one point. If a whole chord and its perpendicular bisector of one side of Spee’s curves occupy a two-dimensional space, then, the perpendicular bisectors of the two whole chords of Spee’s curves on both the sides of the mandible intersect at one point, and this point displays a three dimensional space location. This is the rotation centre of a sphere. Therefore, a similar geometric construction can be applied to produce a sphere having a common centre of rotation with Monson’s sphere, as previously described based on Spee’s curves (Figure 1). The hard framework of the maxillo-mandibular-dental system, which has been described variously as spherical, triangular, conical and circular in its morpho-physiologic state, is meaningless without the input of the oro-facial muscular investments according to Bernard Jankelson – the father of Neuromuscular theory of occlusion [15][16]. A regular tetrahedron is a polyhedron formed from four equilateral triangles (Figure 2). It has four surfaces, four vertices and six edges. The four surfaces are equilateral triangles; and any of the surfaces can act as the base while any of the vertices can act as the apex. Although, a tetrahedron is a three-dimensional geometric object, it shares similar characteristics with equilateral triangle which is a two-dimensional geometric object (Figure 2b) and (Figure 3) [17]. Like a triangle which is characterized by circumcircle, incircle and excircle (Figure 4), a tetrahedron is associated with circumsphere, midsphere, insphere and exosphere (Figure 5) [18][19][20]. For any tetrahedron there exists a sphere (the circumsphere) such that the tetrahedron’s vertices lie on the sphere’s surface (Figure 5). Every triangular surface of a tetrahedron has a circumcircle, incircle and excircle (Figure 4). | ||||||
| ||||||
| ||||||
| ||||||
| ||||||
| ||||||
| ||||||
| Evaluation of the hypothesis | ||||||
|
The evaluation of this hypothesis will be carried out in eight sections:
| ||||||
| Section 1: Implications of the hypothesis | ||||||
|
The implications or consequences of this hypothesis are as follows:
| ||||||
| Section 2: Inter-relationship between form and function | ||||||
|
It is important to note that the morphology of any organ of the human body is determined by the genetic code of the person. However, the final definite characteristics are shaped by internal and environmental influences. There have been a lot of controversies whether form follows functions or function follows form; and it is difficult to address this issue. Nevertheless, there is a link between form and function as far as design principles are concerned. In any structural design, functional consideration forms the bedrock of the planning and execution of the design. Therefore, it can be said that function determines form during construction of the structure as well as having influence on its operational mode. However, it must also be noted that the final product of the design also has a profound influence on its functional performance [21]. From study of the evolutionary development of the skull, facial skeleton and maxilla-mandibular-dental system, it is possible to note that, with advanced development, their structure tends more and more to acquire spherical characteristics. This is particularly emphasized in humans and results from the formation of masticatory apparatus on a background of a variety of chewing movements which become necessary due to the growing diversity of the food eaten [21]. Therefore, certain authors believe it is proper to consider the problem of occlusion, particularly in the construction of the dental rows in dentures for toothless patients, from the stand point of the spherical characteristics of the structure of the human maxillo-mandibular-dental system and the skull on the whole [21]. The basic building blocks of a structure may not be apparent while looking at the whole structure because of the tendency of the whole structure to consume the individual characteristics of the basic building blocks. One of the most important considerations in the design and construction of a functional structure, because it is subjected to functional forces throughout life time, is adequate stability. Therefore, it is appropriate that this complex system should be built on the principles of platonic solids which are known for their stability. One of the five platonic solids upon which many structures are built is tetrahedron. The principles of stability associated with platonic solids have been employed in the fields of chemistry, electricity and electronics, engineering, geology and many other science related disciplines [17]. In geometry, a tetrahedron is a polyhedron composed of four triangular surfaces, three of which meet at each vertex, it has six edges and four vertices and four faces. A tetrahedron is also known as a ‘triangular pyramid’. For any tetrahedron there exists a sphere (circumspehre) such that the tetrahedron’s vertices lie on the sphere’s surface [17][18][19][20][22][23][24]. The faces, vertices and edges of the resulting tetrahedron, constructed by joining the spatial points of Spee’s curves [5] and Monson’s sphere, [6][7] Bonwill’s equilateral triangle [3][4] and Hall’s cone, [8][9][10] can be used to describe the morphological features of the basic elements (TMJ, masticatory and facial muscles, jaws and facial bones and teeth) of the maxillo-mandibular-dental system. These separate elements are characterized by spherical, triangular and conical shapes which are the hallmarks of a tetrahedron. Therefore, it is not by accident that these shapes pervade the morphological architecture of the elements of the maxillo-mandibular-dental system; but the reason for the design can be attributed to the established interdependence and inter-relationship between function and form for the purpose of providing harmoniously integrated activity during functional movements. | ||||||
| Sections 3: TMJ anatomy versus tetrahedron characteristics | ||||||
|
The temporomandibular joint consists of two articulations connected by the mandible. It is known as coupled, since movements occur in both articulations at same time [23]. The temporomandibular joint is formed by the articular fossa of the temporal bone and the condyle of the mandible. Each of the two articulations has an intra-articulator disc, an articular capsule and ligaments. The head of the condyle of the mandible are convex anterio-posterioly and medio-laterally. If the heads of the condyles are considered with their necks, they form conical shapes. The convexity of the head of condyle is an expression of a segment of the circum-sphere of a tetrahedron; and the concavity of the glenoid fossa provides easy movement of the spherical segment. | ||||||
| Section 4: Tooth morphology versus tetrahedron’s characteristics | ||||||
|
A close examination of the crowns of the posterior teeth reveals similarities between a tetrahedron and occlusal appearance of premolars and molars. Each cusp on a premolar or molar is like a tetrahedron. In these multi-cuspate teeth, the cusp fused together during ontogenesis. The tip of the cusp represents one of the four vertices of a tetrahedron while the remaining three vertices of the cusp lie at the base of the cusp. The mesial, the distal and the triangular ridges of the cusp also represent three of the six edges of a tetrahedron while the remaining three edges also lie at the base of the cusp. The two inclined planes of the triangular ridge constitute two of the four triangular faces of a tetrahedron; while the remaining two triangular planes are hidden at the base and the buccal or lingual surface of the cusp. The buccal or lingual curvature of a cusp is a segment of the circumsphere of the tetrahedral shape. The incisors and canines also exhibit morphological features that are similar to a tetrahedron. Every triangular surface of an incisor or a canine is associated with three additional triangular surfaces from which a three-dimentional structure of tetrahedron can be constructed. It should be noted that every curvature associated with these teeth represents a segment of the circum-sphere of a tetrahedral shape. The expression of a tetrahedron’s geometric characteristics as cusps, ridges and inclined planes on the occlusal surfaces of posterior teeth and incisal edges of anterior teeth is a stereo-morphologic structural design to enhance stability for the purpose of preventing excessive movement beyond the limit that can be tolerated by the temporomandibular joints. The inclined planes and ridges of the cusps of posterior teeth as well as the edges of the anterior teeth act as guidances and stoppers to constrain movement of the temporomandibular joints within a tolerable limit of the ligaments and muscles of mastication and facial expression [3][25]. | ||||||
| Section 5: Jaws and other facial bones versus tetrahedron’s characteristics | ||||||
|
The mandible is an unpaired bone with a body, two rami, two condylar processes, two coronoid processes and one alveolar process with the teeth distinguished in it. The mandible is the only mobile bone in the facial skeleton and it is the site of attachment of many muscles which cause its movement. This specific feature of mobility determines its complex structure and influences the development of the facial skeleton and overlaying soft tissues [21]. The maxilla’s construction, as a functional structure, is considered with respect to abutments which are supports that receive the pressure of mastication and the impact suffered when the upper and lower teeth are brought together. Four abutments are distinguished namely: fronto-nasal, zygomatic, pterygopalatine and palatine. These facial bones are designed to form a tetrahedron upon which the maxilla rests. The palatine processes form the horizontal abutments while the other three abutments are vertical columns for transmission of vertical occlusal forces to the cranium. The mandible and maxilla, together with their dental rows which are supported by alveolar processes, are U-shaped or somewhat spherical in shape in conformity with the characteristic features of a tetrahedron [21]. | ||||||
| Section 6: Morphological features of orofacial muscles versus tetrahedron’s characteristics | ||||||
|
The morphological topographies of the muscles of orofacial region in terms of arrangement, shape and orientation are similar to the geometric characteristics of tetrahedron. The infra-hyoid group of muscles is triangular in shape and they are arranged in conical shape with apex of the cone located at the hyoid bone. The supra-hyoid group of muscles are also triangular in shape and they are also arranged in conical shape with the apex of the cone located at the hyoid bone and base of the cone located at the floor of the mouth. The arrangement of these muscles also creates triangular spaces such as submandibular, submental, carotid and muscular triangles in the anterior cervical region [21]. The tongue and the masticatory muscles are triangular as well as conical in shape. The upper and lower jaws, together with their dental rows, are located in between two muscular screens or shields. The outer screen is made up of buccinators, orbicularis oris and other muscles of facial expression. The posterior aspect of the outer screen is completed by the superior pharyngeal constrictor. The inner screen is made up of the tongue and its external muscles. Anteriorly, the outer screen has an opening that separates the orbicularis oris into upper and lower lips thus creating an entrance into the mouth proper. Posteriorly, there is an opening in the inner screen thus creating an entrance into the pharynx and larynx. These muscular screens are designed to keep the relative positions of the jaws and their dental rows and they also act as circumsphere for the hard tissue framework of the maxilla-mandibular-dental system [21]. | ||||||
| Section 7: Special cases of tetrahedron versus morphological variations in the elements of maxillo-mandibular-dental system | ||||||
|
Nature is replete with symmetrical and asymmetrical geometric structures with respect to design. However, some structures that appear to be symmetrical may not be symmetrical after all. Studies have shown some degree of asymmetry in what appears to be symmetrical in human structures [21]. For example, the asymmetry in the structure of the left and right halves of the face is displayed by the following signs: [21]
The resulting tetrahedron derived from interconnectedness of Spee’s curves, Monson’s sphere/curve and Bonwill’s triangle is regular [17]. However, there are other tetrahedral shapes that are irregular. A regular tetrahedron is one in which all four surfaces are equilateral triangles; and it is one of the platonic solids [17]. An isosceles tetrahedron is a tetrahedron where all four surfaces are congruent triangles. In a tri-rectangular tetrahedron, the three face angles at one vertex are right angles. If all three pairs of opposite edges of a tetrahedron are perpendicular, then it is called an orthocentric tetrahedron. When only one pair of opposite edges is perpendicular, it is called a semi-orthocentric tetrahedron. These are some of the well-known irregular tetrahedrons. The irregularities observed in these irregular tetrahedrons, with respect to the length of edges, size of triangular surfaces, angles and other features, can also be seen in the observed variations in TMJ, muscles, jaw bones, cuspal features of posterior teeth and incisal edges and surfaces of anterior teeth. These irregularities are reflections of imperfections in nature as well as deliberate structural or architectural designs for functional efficiency and effectiveness. | ||||||
| Section 8: Testing of the hypothesis | ||||||
|
This hypothesis can be tested, to refute or confirm some of its consequences or predictions, by determining the intercondylar distance of a sample of patients for the purpose of derivation or construction of Bonwill’s equilateral triangle which in turn will be used for the construction of a tetrahedron for each patient. The height of the obtained tetrahedron for each patient can be calculated using Pythagorean theorem, and the obtained value can be compared with the measured rest vertical dimension of the concerned patient for the purpose of finding any correlation between calculated height of the tetrahedron and the measured rest vertical dimension. | ||||||
|
CONCLUSION
| ||||||
|
The tetrahedral geometric framework of the maxillo-mandibular-dental system may not be apparent because of the tendency of the whole system to consume the characteristics of the building blocks of its internal structure. However, a systematic and detailed examination of the various elements of the maxillo-mandibular-dental system reveals the presence of spherical, conical and triangular shapes which are the main geometric shapes associated with a tetrahedron. The triangular faces, vertices and edges of a tetrahedron are similar to the morphological expressions of the muscles of orofacial region, the jaws and other facial bones and the teeth. These morphological expressions emphasize the integration of mechanical and neuromuscular schools of thought on occlusion as well as the need for mechanical and neuromuscular elements of the orofacial complex to act harmoniously to produce the desired results. Thus, the various established theories and concepts of occlusion can adequately be described and explained using the tetrahedron’s characteristics. Consequently, a new theory of occlusion to be called “the tetrahedral theory of occlusion” or “the unification theory of occlusion” is hereby presented to the dental professionals for further objective critique. | ||||||
|
REFERENCES
| ||||||
| ||||||
|
[HTML Abstract]
[PDF Full Text]
|
|
Author Contributions
Adolphus Odogun Loto – Substantial contributions to conception and design, Acquisition of data, Analysis and interpretation of data, Drafting the article, Revising it critically for important intellectual content, Final approval of the version to be published |
|
Guarantor of submission
The corresponding author is the guarantor of submission. |
|
Source of support
None |
|
Conflict of interest
Authors declare no conflict of interest. |
|
Copyright
© 2017 Adolphus Odogun Loto. This article is distributed under the terms of Creative Commons Attribution License which permits unrestricted use, distribution and reproduction in any medium provided the original author(s) and original publisher are properly credited. Please see the copyright policy on the journal website for more information. |
|
|
|
ABOUT THE AUTHOR
| ||||
| |